ラプラス分布

ラプラス分布（ラプラスぶんぷ、英: Laplace distribution）は連続確率分布の一つで、二重指数分布（英: double exponential distribution）、両側指数分布とも呼ばれる。ラプラス変換で有名なフランスの数学者ピエール＝シモン・ラプラスによって名付けられた。

定義と性質

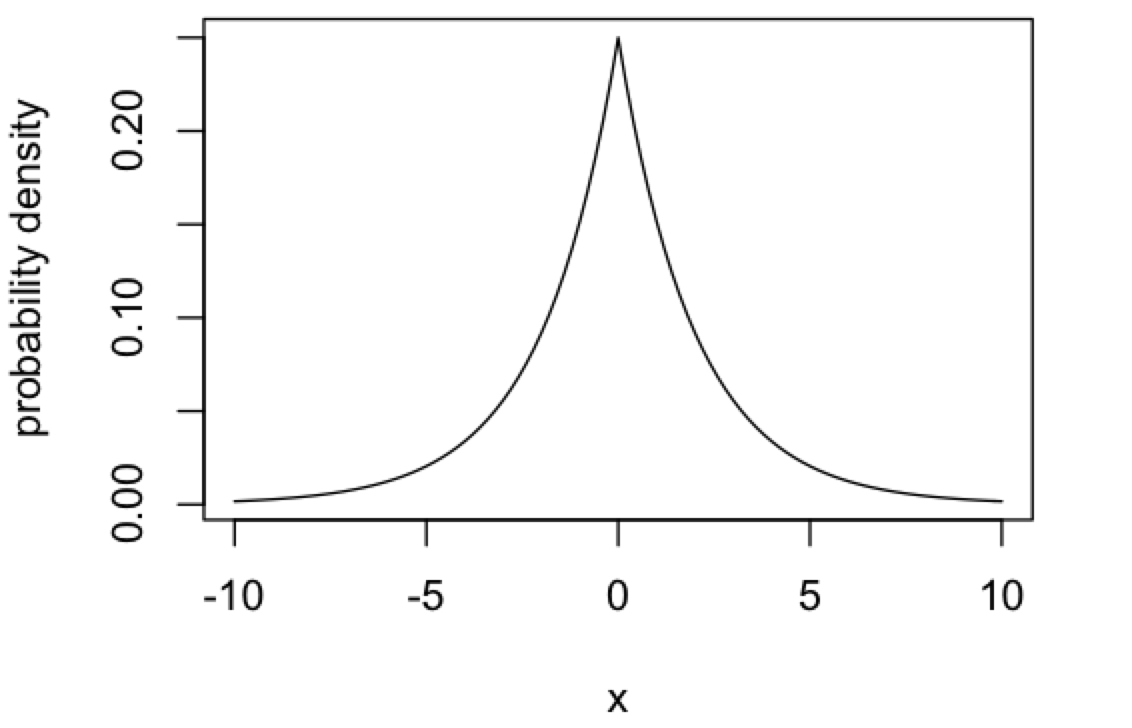
確率変数を実数 x (−∞ < x < ∞) とするときのラプラス分布の確率密度関数は以下の式で定義される。

${\displaystyle f(x;\mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)}$

位置母数 ${\displaystyle \mu }$、尺度母数 ${\displaystyle b}$ について、

${\displaystyle f(x;\mu ,b)={\frac {1}{b}}f\left({\frac {x-\mu }{b}};0,1\right)}$

累積分布関数は

${\displaystyle {\begin{aligned}F(x;\mu ,b)&={\begin{cases}{\dfrac {1}{2}}\exp \left({\dfrac {x-\mu }{b}}\right)&(x<\mu )\\1-{\dfrac {1}{2}}\exp \left(-{\dfrac {x-\mu }{b}}\right)&(x\geq \mu )\end{cases}}\\&={\frac {1}{2}} {\frac {1}{2}}\operatorname {sgn} (x-\mu )\left(1-\exp \left(-{\frac {|x-\mu |}{b}}\right)\right)\end{aligned}}}$

期待値は μ、分散は 2b² である。歪度は 0、尖度は 3 である。

サンプリング

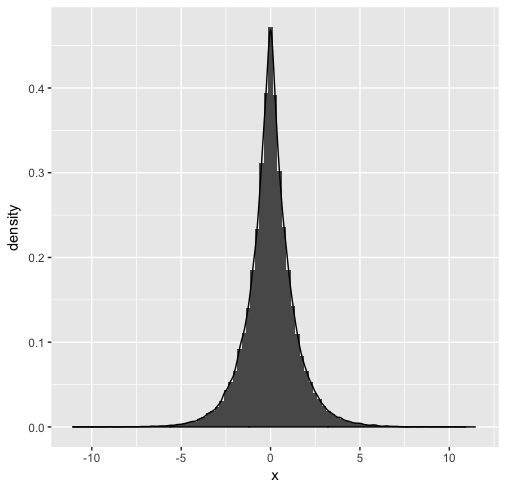
ラプラス分布の標本は以下の手法でランダムサンプリングできる。

逆関数法

ラプラス分布は逆関数法を用いることで一様分布からランダムサンプリングできる。

累積分布関数 ${\displaystyle y\ (0\leq y\leq 1)}$ の逆関数は ${\displaystyle u=y-1/2\ (-1/2\leq u\leq 1/2)}$ を用いて次のように表される。

${\displaystyle x=\mu -b\operatorname {sgn}(u)\ln(1-2\left\vert u\right\vert )}$

ゆえに一様分布からのサンプリング値 ${\displaystyle u\sim U(-1/2, 1/2)}$ を代入してラプラス分布からのランダムサンプリングが実現できる。

参考文献

• 蓑谷千凰彦、統計分布ハンドブック、朝倉書店 (2003).
• B. S. Everitt（清水良一訳）、統計科学辞典, 朝倉書店 (2002).

関連項目

• 確率分布

外部リンク

• Laplace Distribution -- from Wolfram MathWorld